彻底弄明白CRC校验

CRC是应用广泛的检错码，全称是“循环冗余校验码”，也称为多项式编码。

1. CRC校验的数学原理

数学用简洁的公式描述了自然界事物的基本规律，数学之美，一切皆来源于数学！先回顾下数学中多项式中的乘除法（下面我们只讨论系数为0或1的多项式）：

先看个多项式除法的例子：商是 $\chi{2}+1$，余数 $-1$.
$$
\frac{\chi{3} + \chi{2}+\chi}{\chi+1} = (\chi{2}+1) …(-1)
$$
等价于：
$$
(\chi{2}+\chi+1)\chi = (\chi{2}+1)(\chi+1)-1
$$

多项式系数映射为二进制数，用二进制除法来求这个多项式的解；多项式映射到二进制数的方法：

被除数 $\chi{3} + \chi{2}+\chi$ 写成 $\chi{3} + \chi{2}+\chi+0\chi{0}$；取多项式系数，即转成二进制数 $1110$ 。

同理 除数$\chi+1$ 等价于 $11$ .

二进制除法（以2为模完成，加减法都无进位和退位，等同于异或操作）：

如上图手算，商的二进制表示为 $101$ 对应多项式 $\chi{2}+1$ , 余数为 $-1$ ，（可以看到二进制1110b转成十进制为14，11b为3，$14/3=5…-1$）。

上面说明了系数为1或0的多项式除法与二进制数异或操作的一些联系，我们将利用它来设计CRC校验码的生成。
$$
(\chi{2}+\chi+1)\chi = (\chi{2}+1)(\chi+1)-1
$$
$\chi{2}+\chi+1$ 表示了原始信息111，除式$\chi+1$ 是所谓的 CRC_KEY，余数1就是所谓的CRC校验值，真正的被除数是原始信息本身乘上除式最高次$\chi{1}$得到的 $(\chi{2}+\chi+1)\chi$，也就是1110，末尾补上除式的最高次个零，$\chi{16}$ 就补上16个零。

发送方计算出CRC校验值后，用原始信息减去校验值
$$
M(\chi)*\chi{n} = Q(\chi)*K(\chi) - R(\chi)
$$
$M(\chi)$ 是原始的信息多项式，$K(\chi)$ 是 n 阶的CRC_KEY 多项式，$M(\chi)*\chi{n}$ 表示将原始信息后加n个0。$R(\chi)$是余数多项式，即计算出的CRC校验值。

发送双方协商好一个共同的 $K(\chi)$，发送者将$M(\chi)*\chi{n} + R(\chi)$ 发送出去，接收者收到数据通过能否被 $K(\chi)$ 整除来校验数据的完整性，是否有错误位发生。

了解到CRC校验原理后，我们可以想象到其检错能力一定与除数多项式$K(\chi)$的长度有关，后面我们称 $K(\chi)$ 为CRC的多项式。

2. 手算CRC校验值

此部分以实例来说明CRC的计算方法；取信息原始值为0x5A1301，多项式为 $\chi{16}+\chi{12}+\chi{5}+1$对应二进制 $10001000000100001$，原始值附加16个0，对应二进制$101101000010011000000010000000000000000$，二进制除法如下图所示，我们只关注余数；

CRC计算过程：从原始数据位串高位开始依次与多项式的位串进行异或操作，得到的结果再次与多项式异或，直到长度小于多项式时，结果便是CRC校验值。

余数为$1101111100001110$, 下图为网络工具计算结果，完全一样。

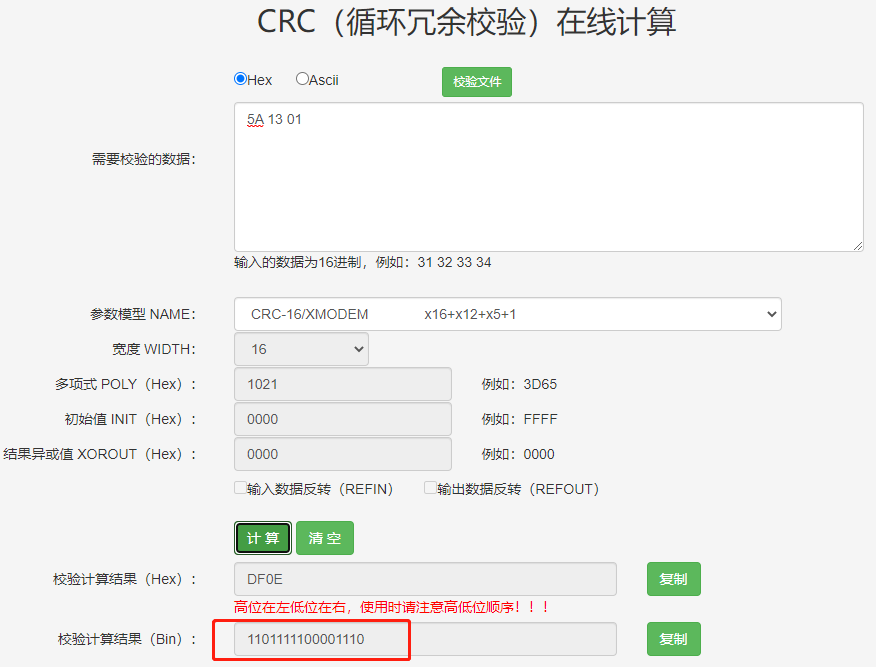
3. CRC代码实现

根据上述手算过程，基于CRC-16的实现代码如下，对原始信息按字节操作，保证每一位都与多项式位串参与运算；也可以看到这里参与运算的多项式位串是10001000000100001，一共17位二进制。

uint16_t iot_calc_crc16(const uint8_t *data, uint32_t size)
{    
    uint16_t crc_reg = 0x0000,tmp = 0;
    uint8_t j,byte = 0;
    
    while (size--){
        byte = *(data++);
        crc_reg ^= byte << 8;
        for ( j = 0; j < 8; j++) {
            tmp = crc_reg & 0x8000;
            crc_reg <<= 1;
            if (tmp)
                crc_reg ^= 0x1021;
        }
    }
    return crc_reg;
}

关于上述代码是如何将多项式位串的最高位参与运算的，请自行揣摩；记住一个规则：多项式位串最高位一定是1。

代码获取：https://github.com/SeeDeer/crc

4. CRC的检错能力

先来看一个例子，如何人为的制造错误，让接收方校验通过。

发送方原始数据(0x5A,0x13,0x01)：1011010 00010011 00000001，进行CRC16_XMODEM 运算后，crc校验值(0xDF0E)：1101111100001110。

发送方发送的数据(0x5A,0x13,0x01,0xDF,0x0E)：1011010 00010011 00000001 1101111100001110，接收方收到后再进行CRC16_XMODEM 运算，如果结果为零，说明校验通过。

好了，我们来人为的制造错误，CRC16_XMODEM的多项式是 $\chi{16}+\chi{12}+\chi{5}+1$ ，对应位串 100010000 00100001，将发送的数据和多项式位串低位对齐，进行一次异或操作得到的数也能校验通过。

原数据	1011010 00010011 00000001 1101111100001110	0x5A,0x13,0x01,0xDF,0x0E
人为制造错误的数据	1011010 00010011 00000000 1100111100111111	0x5A,0x13,0x00,0xCF,0x2F

可以看到，错误发生时，要想校验通过，必须满足错误位刚好发生在除数多项式$K(\chi)$中；除此之外其他错误都能被检测到。

5. CRC校验总结

1. CRC是一种检错码，不具备纠错能力；检测到错误发生时，由重传来处理，用于错误率较低的数据链路，。
2. 数学原理上：将信息的二进制 $k$ 位帧看作一个 $k-1$ 次多项式的系数列表，该多项式有$k$项，从 $X^{k-1}$ 到 $X^0$ 。发送方和接收方约定一个除数多项式$K(\chi)$ ，发送方将原始信息帧多项式乘以$X^{k-1}$后，再除以$K(\chi)$，所得余数 $R(\chi)$即为计算出的CRC校验值；发送时减去余数 $R(\chi)$ 发送。接收方如果接收到正确数据时，将可以被约定的 $K(\chi)$ 整除。依次来完成校验。
3. 整个运算采用异或操作来完成，很多芯片实现了CRC硬件运算单元，提高了运算速度。
4. CRC的除数多项式选取很重要，最高位和最低位系数必须为1。一般采用业界认可的常用多项式。